Tipos de fracciones

¿Qué son las fracciones?

En matemática la palabra fracción se utiliza para hacer alusión a la representación de la división de una totalidad en partes que resulten exactamente iguales entre sí. Es decir, representan una división. Por ejemplo, cuando se dice “me comí media pizza” se asume que la misma está cortada en dos partes iguales y que la persona se comió una de esas porciones. En cifras, esto se representa poniendo un número abajo del otro, o al lado, separados por una barra. De esta manera, la persona podría representar numéricamente que comió media pizza de la siguiente manera: 1/2.

Las fracciones: sus partes

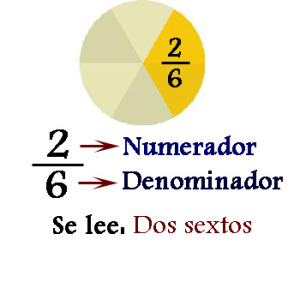
Así, dentro de la fracción se pueden identificar tres partes que la componen. Por un lado, el nominador, que es el número que se coloca arriba o delante de la barra. Este número es el que representa las cantidades de las partes que se han tenido en cuenta con respecto a una totalidad. En el caso de la pizza antes mencionado, sería el 1. Esto significaría que sólo se toma una de las partes del todo, o sea, una porción. El denominador, por otro lado, es aquel que representa en cuántas partes idénticas se ha dividido el entero. En el caso de la pizza es el dos, es decir, que la pizza se dividió en dos porciones. La línea que separa a ambos números se la conoce bajo el nombre de barra de fracción. De esta manera, toda fracción tiene tres partes básicas.

(Las partes de la fracción)

Clasificación de las fracciones

Dentro de las fracciones, se pueden identificar distintos tipos. Algunos de ellos son los siguientes:

Si se toma en cuenta los valores que adquieren el denominador y el numerador, se habla de dos variedades de fracciones:

1. Impropias: esta clase de fracciones es la que se identifica por contar con un denominador cuyo valor es menor que el del numerador. Algunos ejemplos podrían ser los siguientes: 3/1; 99/22; 12/10; 15/5 o 4/2.

2. Propias: en oposición a las fracciones impropias, en las propias, el nominador tiene un valor menor que el del denominador, como sucede en los siguientes ejemplos: 2/3; 4/9; 11/17 o 20/44, entre otros.

 Otras clasificaciones

También, existe un determinado tipo de fracciones que se caracterizan por no poder simplificarse más. Es decir, que no pueden ser divididas por ningún otro número, como ocurre en los siguientes ejemplos: 11/13; 7/9 o 1/2. A estas fracciones se las conoce como irreductibles.

Si se relacionan al menos dos fracciones entre sí, también se pueden establecer otro tipo de fracciones y son las que se denominan Equivalentes. Esto se da cuando en dos fracciones, al multiplicar sus números en forma de cruz, se obtiene el mismo resultado. Esto quiere decir que si se multiplica el denominador de una por el multiplicador de otra y a la vez, el multiplicador de la primera por el denominador de la segunda, se obtiene el mismo resultado.

Pongamos unos ejemplos: 3/4 y 4/3. En este caso, multiplico el 3 del denominador de una de las fracciones por el 4 del nominador de la otra y me da 12. Y, si multiplico el 4 del denominador de una por el 3 del denominador de otra, también me da 12. Es decir, son fracciones equivalentes. Otro ejemplo sería: 3/2 y 6/4. En este caso, también cuando se multiplica en forma de cruz, el resultado final es de 12, por lo que también se trata de fracciones equivalentes.

Formas de obtener fracciones equivalentes

Existen dos caminos diferentes para obtener esta clase de fracciones. Por un lado, se habla de la simplificación. Esto significa que se dividen al numerador y al denominador por el mismo número. De esta manera, la fracción que dé como resultado será equivalente a la multiplicada. Un ejemplo podría ser el siguiente: tomar la fracción 10/12 y dividir ambas cifras por 2, lo que daría el siguiente resultado: 5/6. Al multiplicar en forma de cruz 6 x 10 y 5 x 12, en ambos casos el resultado sería 60, por lo que estamos frente a fracciones que son equivalentes entre sí.

Otro método para obtener fracciones equivalentes es a partir de la amplificación. Esto significa multiplicar al numerador y al denominador por el mismo número. Como por ejemplo en el siguiente caso: 2/3 x 3/3 = 6/9. Se puede decir entonces que 2/3 y 6/9 son equivalentes. Esto es porque al multiplicar de forma cruzada, en ambos casos el resultado obtenido es 18.

Más tipos de fracciones

• Otras fracciones que se pueden identificar son las fracciones decimales, que son aquellas cuyo denominador tiene la característica de ser una potencia de 10, como sucede en los siguientes ejemplos: 5/10; 15/100 o 2/1000.
• También se habla de las fracciones mixtas, que son aquellas que están compuestas por un número entero y el otro fraccionario. Como por ejemplo 3 6/7 o 2 7/8. El tres y el 2 son números enteros y 6/7 y 7/8 los fraccionarios.